大 O 符号基础知识变得非常简单
关于大O的简短对话
关于大O的简短对话
说实话,我刚开始编程的时候,因为害怕而拖延了好一阵子学习 Big O,这篇文章真的适合所有有类似感受的人。我不知道这样说对不对,大部分内容都是常识,数学方面也没什么比乘法难的了。但为了以防万一,我会添加一些视觉效果,尽量让阅读过程不那么痛苦。这些图看起来有点傻,但说实话,它们能帮助我记住一些东西。
如果我要给你一个最简单的版本来解释大 O 符号背后的想法,或者代码运行的时间复杂度,那将是这样的:
- 基本操作是最有效的
- 重复操作(循环)可能会对效率造成更大的担忧
- 嵌套循环是效率方面最大的隐患之一
说实话,这些都是基础知识。还不错吧?在评估代码性能时,还有一整类你根本不用考虑的事情。你可以把它们看作是“免费赠品”。它们包括:
- 基础数学、加法和减法
- 分配变量
- if/else 条件
- 声明一个函数
- 调用函数(表面上)
- 改变变量
如果要我用最简单的术语来概括“大 O”的概念,那么我们担心的几乎就是循环。我知道,当我意识到这一点时,我的恐惧感就减轻了很多。
💡开始前先声明一下:对于那些觉得大 O 符号听起来像陈旧仪式的人来说,这篇文章旨在提供绝对的基础知识。其实还有很多细微差别和描述,比我在这里列出的要多。每当有机会强调清晰度而不是更详细的细节时,我都会选择清晰度。这篇文章是写给刚入行几个月、需要基本可操作信息的编程爱好者的。这篇文章是我正在写的关于现场编程面试的系列文章的一部分,所以也推荐你读一下这个系列文章 🤓
为了解释其中的一些内容,我们假设我在空闲时间喜欢玩寻宝游戏。我的朋友们为这些寻宝游戏制定规则,有些规则难度较低。(补充一下,有些人真的这么做!有一种叫做地理藏宝的爱好,它几乎就是现实生活中的寻宝游戏。如果你感兴趣的话,可以在这里阅读相关内容。不过,我举的例子太傻了,不符合真正的地理藏宝游戏的规则,所以我就用寻宝游戏这个词吧)。
第一部分:常数时间或 O(1)
🏴☠️ Jamie 让我去寻宝,去 Chestnut 街的某个地址找一支钢笔。我只有一个地址,所以只需要去一户人家,超级简单。
这就是我们所说的“恒定时间”的一个例子。无论寻宝游戏是寻找钢笔还是其他什么东西,在这个场景中,我只敲了一扇门,门不会改变。这对于算法性能来说是一个非常积极的状态,实际上是最优的。恒定操作的一个例子是从 JavaScript 对象中检索值。
const person = {
name: "Ann",
hobbies: ["drawing", "programming"],
pet: "dog"
}
console.log(person.name)
因为 JavaScript 对象本身就是一种哈希,所以在对象中查找某个值的性能非常高。这完美地模拟了拥有一个精确的地址,并且能够直接找到它而无需进一步搜索。无论对象中的内容是什么,检索该值的步骤都被认为是在恒定时间内运行的。
💡因此,对象/哈希数据结构通常是代码挑战中的好朋友。
有时,将数组转换为对象格式可以极大地提高这类挑战的性能。我们称之为常数时间 O(1),用大 O 表示法表示。
第 2 部分:对数时间,或 O(log N)
🎁 我的朋友杰克给我布置了一项更棘手的任务。我家附近正在建一个新楼盘,但他们没有安装醒目的路牌。不过,如果我走到那些房子前,他们把地址写在了前门的横梁上。
我其实并不想逐一走到每一家每户,但经过思考后,我意识到杰克曾说过,随着你沿着街道前进,家庭住址号码会增加。
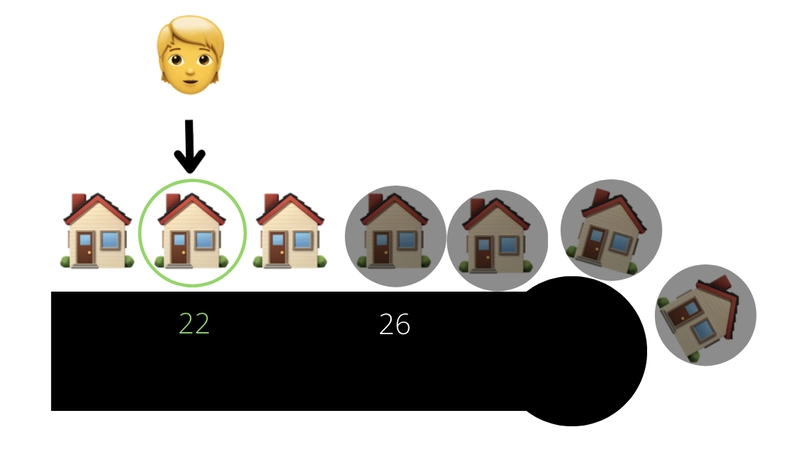
我不知道起始门牌号,因为这条路从相反方向延伸出去还有很长一段路,所以我不确定最低的门牌号是多少。但我知道我要找的是22号。我意识到,如果我从街道中间开始,就能知道地址是比我要找的低还是高,这样就能排除掉街区里一半的房子,这样我就不用再搜索那些房子了。
我看到中间的房子是26号,所以这栋房子右边的所有房子的门牌号都太高了,不符合我要找的22号。所以我可以划掉我走到的那栋房子,以及右边所有的房子,因为它们的门牌号更高。
在正常情况下,这些房子都是常规的,我可以直接数到正确的房子。但我看到一些空地,不知道它们是否也会被改造成住宅,或者用于景观美化或公园。因为我不太确定什么是地块,所以我不确定直接沿着街道数到正确的房子是否可行。
所以我决定再次采用“从中间选”的方法,这样至少可以根据房屋编号过高或过低来跨越剩余路段的一半。因此,我再次从剩下的三栋房子中选择了中间那栋。
你知道吗!答案是对的。如果你想理解我的“寻宝算法”,最终结果相当不错。虽然街上有七栋房子,但我最终只需要走到两栋。就我完成这项任务所需的工作量而言,我的方法意味着,每走到一栋房子,剩下的待搜索房屋数量就会减少一半。
我们将每次缩减结果集时的性能称为对数性能,在常数时间 (O(1)) 内,这是最理想的性能。即使结果集有 7 个,执行的操作也可能只有 2 次。如果您不太记得数学上的对数知识,那也没关系——您只需知道,对于一个算法来说,这已经是相当出色的性能了,因为每次缩减结果集都会显著减少。
在 Big O 语言中,我们将对数性能写为 O(log n)。如果你担心记不住 Big O 描述符,那么在面试中直接称之为“对数时间”完全没问题。如果你只需要知道对数时间意味着每次迭代都可能将结果缩短一半,那么在实际操作中很容易就能意识到这一点。
补充一下:我的寻宝游戏示例是一个二分搜索算法的例子。还不错吧?只需从中间反复挑选即可。如果你知道结果已经按某种顺序排列,那么这是一个很好的算法。
第 3 部分:线性时间,即 O(n)
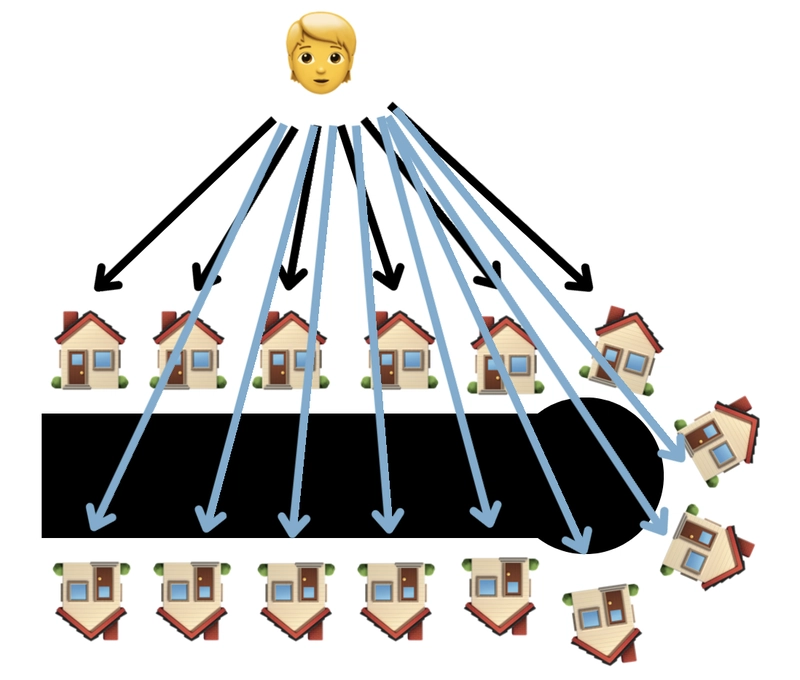
🍬我的朋友杰西听说我为这些寻宝游戏付出了这么多努力,很同情我。幸运的是,那天正好是10月31日,她给我布置了“不给糖就捣蛋”的任务!我的寻宝任务是去梧桐街上每家每户讨一块糖。
在这张故意弄得有点混乱的图表中,你可以看到与我上一个任务相比,这项工作需要做多少工作。
这就是我们在大 O 中所说的“线性时间”,也就是循环,也就是简单的乘法。我的任务量乘以房屋数量。在一条更宽阔的街道上,可能需要往返 50 次。我的工作量会根据我所在的街道和房屋数量线性增加。
对于大 O 算法,线性时间在很多情况下都是一种不错的算法性能。虽然不如我们之前介绍的前两种算法那么好,但通常情况下,你在面试中遇到的代码挑战足够复杂,因此很有可能需要循环。我们将其记为 O(n),其中“n”基本上是你要乘以的数,或者你需要执行的循环次数。
第 4 部分:二次和三次时间
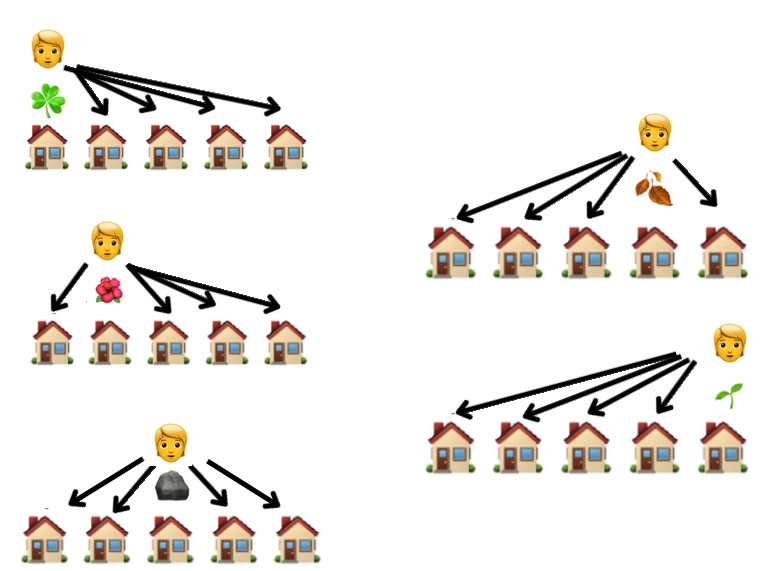
👿 我上一个朋友安德鲁真是个狡猾的家伙,他让我去寻宝,这可是他迄今为止最难的。他带我去了大街,说街上每家每户都要找一样东西,看看能不能在每家找到一样东西。
很快我就完成了25个独立任务,因为我要为五栋房子分别做五件事。你可以很容易地看出,如果用数字来表达,我有5 x 5个任务,也就是5^2个。这就是我们所说的“二次方时间”。
在编程中,这意味着一件事:嵌套循环!每一层嵌套循环都会增加一个指数。如果我的朋友说我想让你对不止一条街道执行此操作,那么数学运算就会变成“街区 x 房屋 x 物品”之类的东西,并且很容易变成立方时间,即 O(n^3),这在现实生活中通常以第三个嵌套循环的形式出现。
我的例子还是比较容易处理的,但在实际编程中,我们遇到的数字要大得多。看看任务是如何膨胀的:
| 基数 | 任务^2 | 任务 ^ 3 | 任务 ^ 4 |
|---|---|---|---|
| 100 | 10000 | 1000000 | 100000000 |
| 1000 | 1000000 | 10亿 | 1000000000000 |
| 100000 | 10000000000 | 1000000000000000 | 100000000000000000000 |
| 1000000 | 1000000000000 | 1000000000000000000 | 1000000000000000000000000 |
这也许是我能和你讨论的最重要的领域了。它在我的工作和编程中出现得最多。你很快就能明白为什么它如此重要。
你会注意到,如果不小心处理嵌套循环,基数为 100 的第一行很快就会比基数为 100 的最后一行执行更多的操作。拥有百万级数据集的人,其程序执行的工作量可能比拥有 100 条记录数据集的人要少,这完全取决于他们对嵌套循环的谨慎程度。
在代码挑战中,我遇到的大多数细节问题是,我能否将循环中的某些内容转化为常数时间,以及我能否将嵌套循环中的某些内容转化为单个循环中的某些内容。(也就是说,从三次方时间 O(n^3) 到二次方时间 O(n^2))。 *
我们还有一个更通用的词来表示指数为 n 次方的情况: *指数时间 (O(2^n))。
第五部分:未来可能是什么样子
假设我们收到以下代码挑战。
Given an array of unique integers and a target number, determine if any two
numbers in the array when added together would equal the target. If that
condition is met, return the array position of the two numbers. You cannot
reuse a number at a single index position (So array [4,2] could make
target number 6, but array [3] could not since it would require reusing the
array value at position array[0]).
Example: given array [1, 2, 3, 4, 5, 6] and target number 10, you would return
an answer [3, 5] since at array[3] you have number 4, at array[5] you have
number 6, and added together they make 10.
Example: given array [1,2,4] and target number 50, you would return false
because the condition can not be met.
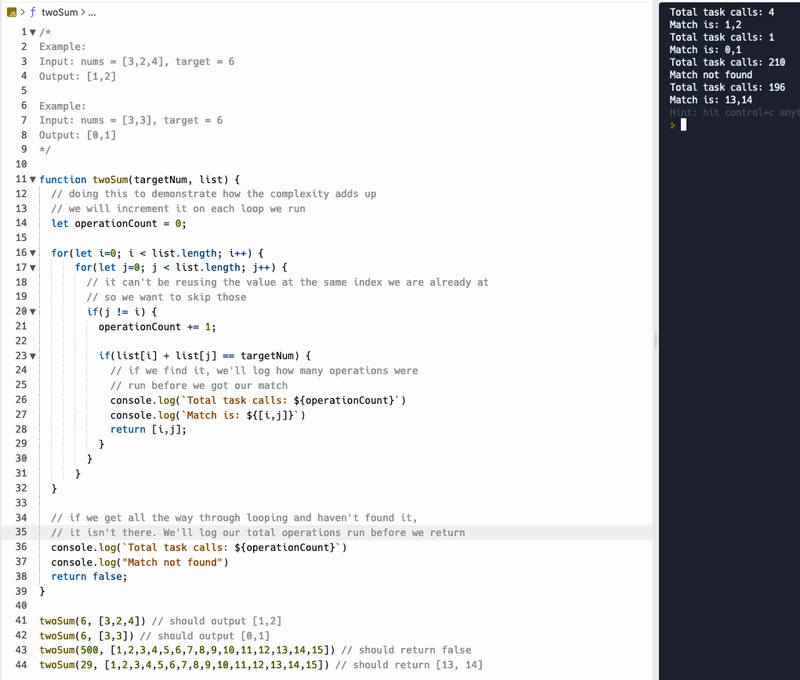
这是一道 Leetcode 题目的释义,题目中接下来会问一个问题:“你能把时间复杂度降到 O(n^2) 以下吗?” 这个问题本身就暗示我们可能做到。但对于一个非常新手的程序员来说,解决这个问题的显而易见的方法可能是这样的。(你也可以自己运行代码,点击此处)。
您可以很快看到,指数逻辑赶上了我们,并且我们在这种方法中有相当多的单独的任务调用。
回到我之前所说的,尝试让事情成形,以便您可以利用恒定时间和线性时间,我将使用所有相同的测试用例,但以更好的 Big O 方式重写此函数。(顺便说一句,这只是说明性的,也许不是我解决这个问题的确切方法,所以不要在评论中找我哈哈)。
在这类问题中,哈希值真的很有用。所以,当我迭代列表时,我会创建一个 JavaScript 对象,其中每个键代表列表项需要添加才能达到目标数量,而值代表我找到该项的索引。
Example: given target number 8 and list [1,2,3,4,9,6] my JS object would
look like this:
{
// first array item is 1, we'd need to find a 7 to make 8, its at index 0
7: 0,
// second array item is 2, we'd need to find a 6 to make 8, its at index 1
// so on and so forth
6: 1,
5: 2,
4: 3,
6: 5
}
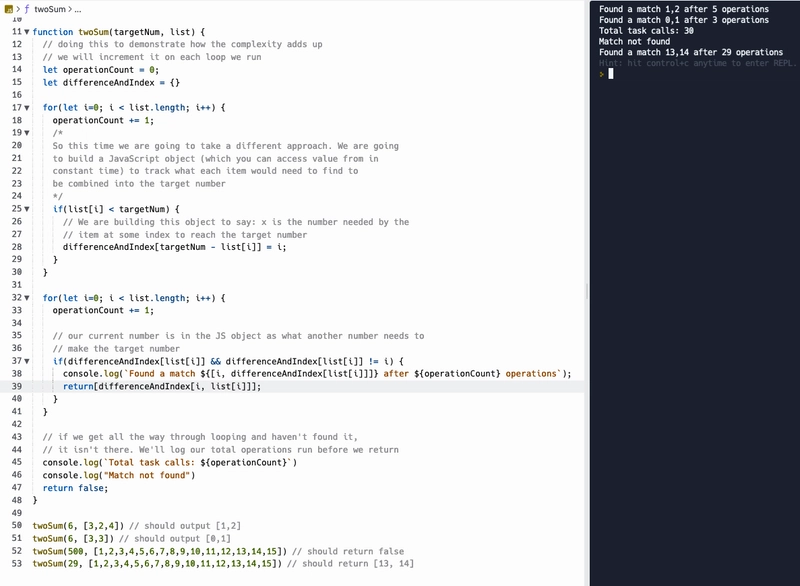
所以有了这个对象,我就不用再做嵌套循环了。我可以再做一个常规循环(也就是线性时间),只需检查当前列表项是否是这个 JavaScript 对象的键值之一即可。如果是,就说明我找到了一个匹配的对,其和就是目标数字。我已经将第一个数字所在的索引保存为键值,这样我就可以直接使用它了,然后在第二个循环中返回当前列表项的索引即可。你也可以在这里试用这段代码。
我使用了相同的测试用例,结果也一样。但是,使用嵌套循环方法时,我们看到的最差性能超过 200 次操作,而使用非嵌套循环方法时,只有 30 次操作!这真是太神奇了。而且,一旦你习惯了这种思维方式,提取嵌套循环的行为并找到其他方法就不难了。
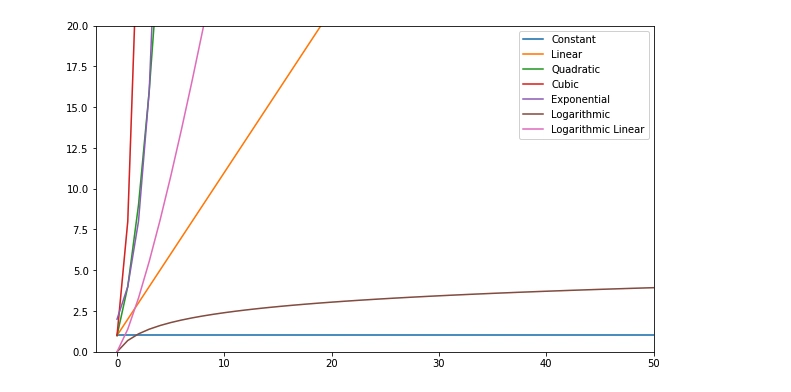
将我们所学到的知识可视化
了解这些性能的一个好方法是查看性能图表,我从这个网站上抓取了这张图表。
另一个有趣的注释
看到上面的问题,你可能会想,既然我们循环了两次,那么大 O 符号是不是 O(2(n))?如果循环是 O(n),那我们就执行了两次:一次是构建 JavaScript 对象,第二次是再次处理列表,看看是否有两个数字的和等于目标数字。
如果你还记得我说过我们主要关心的是循环,那么在这里加一个星号,表示我们关心的是问题中存在的最大运算量。这是什么意思呢?
- 如果你的程序中有一个循环的性能为 O(n),而后面的代码中又有一个嵌套循环的性能为 O(n^2),那么我们把最大的 O 简化为 O(n^2)——指数是程序中最高阶的行为,也就是最大的问题。所以我们去掉较小的那个。
- 如果一个嵌套循环的运行时间为 O(n^2),之后又有一个三重嵌套循环的运行时间为 O(n^3),我们会将其简化为立方时间。由于三重嵌套循环是代码中数量级最高的,所以我们将其简化为 O(n^3)。
仔细想想,这样做更公平。几乎所有你编写的代码都会包含一些 O(1) 的操作,但说程序的整体性能是 O(1) 几乎从来都不准确。如果它只有一个循环,那么这种说法就不准确了。
结论
我们还可以介绍其他类型的大 O 符号,但以上是我最常看到的,它们应该能让新程序员在代码挑战中取得长足进步。即使你对数学概念不太感兴趣,记住循环是你最需要担心的事情,我认为这是一条任何人都能记住的简单建议,而且无论你的编程水平如何,它都能真正帮助你关注性能。
此外,这里还有一些其他很好的资源:
文章来源:https://dev.to/heyjtk/big-o-notation-basics-made-dead-simple-1c9m 后端开发教程 - Java、Spring Boot 实战 - msg200.com
后端开发教程 - Java、Spring Boot 实战 - msg200.com