拓扑排序，解决谷歌面试题

如果我们想成为一名全栈开发人员，我们可以遵循以下路径：

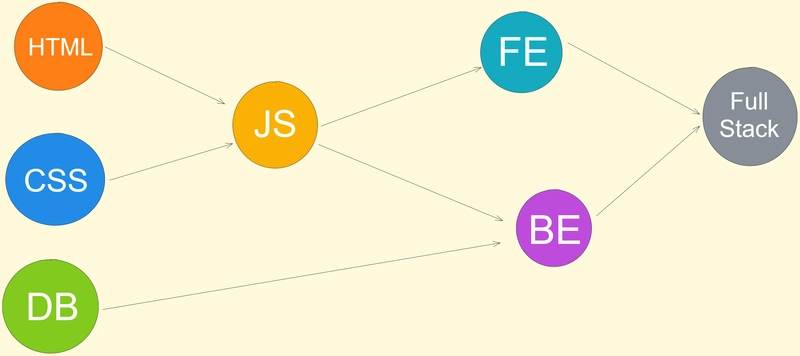
首先，我们学习基础的 HTML 和 CSS，然后学习 JavaScript。之后，这条路径会分为前端开发和后端开发。要成为后端开发人员，我们需要学习数据库，最后成为一名全栈开发人员。

所以这条路是固定的，要学习前端框架，你需要了解 HTML、CSS 和 JavaScript 的基础知识。

组件之间是单向关系，不能先学React再学HTML。

拓扑排序是指事物发生/出现的顺序，在实际生活中有很多用途，例如在处理大数据时，数据以块的形式提供，以便资源利用率达到最优，然后传输处理后的数据。网络中的最大友谊距离（在社交媒体网络上也称为六度分离）是使用拓扑排序来解决的。

现在我们知道了什么是拓扑排序及其用途，让我们来解决 Google 经常问到的一个问题。

X---------------------------------------------X

问题：课程安排

你需要选修的课程一共有 n 门，分别标记为 0 到 n-1。

有些课程可能有先修课程，例如，要修读课程 0，你必须先修读课程 1，这表示为一对：[0,1]

给定课程总数和先修课程对列表，返回完成所有课程应遵循的课程顺序。

给定输入：numCourses（表示需要选修的课程数量）以及 prerequisites 数组（用于确定课程之间的依赖关系）。如果不存在依赖关系，则返回 0。

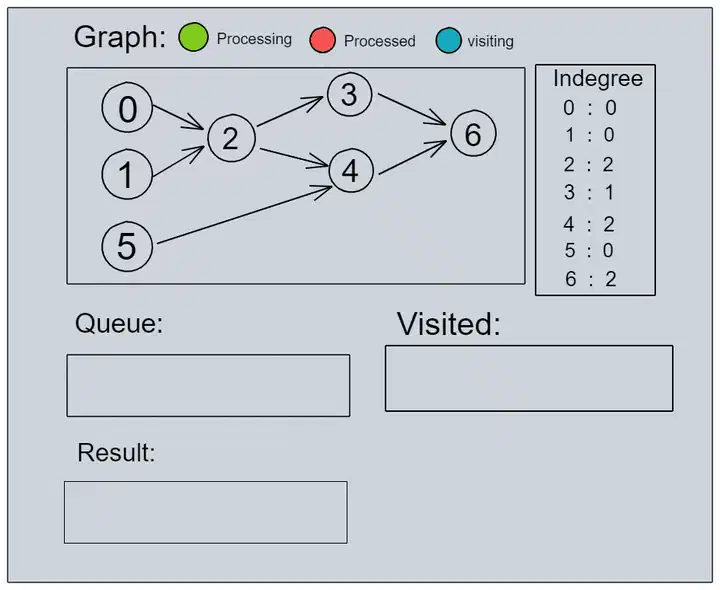
例如：如果给定数据为 [[2,0],[2,1],[3,2],[4,2],[4,5],[6,3],[6,4]]

我们的图表将如下所示：

由此我们可以说可能的顺序可能是：[0,1,5,2,3,4,6]

步骤 1：构建图表

图可以用邻接表/邻接矩阵来表示。两者都很容易实现。在本例中，我们将使用邻接表，因为该图是稀疏图（即许多节点彼此不相连）。

除了我们的图表之外，我们还将维护一个数组，indegree，它将维护节点“i”的先决条件的数量

     var topologyOrder = function(numCourses,prerequisites){

        // create each individual node
        let graph = new Array(numCourses+1);

        // to track the number of dependencies required by each node
        let indegree = new Array(numCourses+1).fill(0);

        for(let i=0;i<numCourses+1;i++){
            graph[i] = []; 
        }

        for(let prerequisite of prerequisites){
            let from = prerequisite[1];
            let to = prerequisite[0];
            graph[from].push(to);
            indegree[to]++;
        }
        console.log(graph);
        console.log(indegree);
  }

操作结束后我们的图表将如下所示：

   graph = [[2]                // 0 -> 2
            [2]                // 1 -> 2
            [3,4]              // 2 -> 3, 2 -> 4
            [6]                // 3 -> 6
            [6]                // 4 -> 6
            [4]                // 5 -> 4
            []]                // 6 -> end   

 indegree = [ 0,               // 0 ie no prerequisites
              0,             
              2,               // 2 courses are required before this
              1,               // 1 course is required
              2,               
              0,
              2 ]

现在我们有了一张图表，它显示了在学习某门课程之前需要完成多少门课程。让我们继续下一步。

广度优先遍历

第一步是选修入度为“0”的课程，即没有先决条件的课程。

此外，我们维护一个队列来处理图中的每个节点，就像我们在 BFS 遍历中所做的那样。

   let queue = [];

   for(let i=0;i<indegree.length;i++){
       if(indegree[i] == 0){
            queue.push(i);
       }
   }

我们的下一步将是处理队列中的每个节点，但在此之前，我们需要确保队列中有要处理的节点。

例如：如果给定的输入是 [[0,1],[1,0]]，即 0 -> 1 和 1 -> 0。我们陷入了死锁。

   if(queue.length == 0) return 0;

下一个问题是如何处理节点？同时，我们必须确保流程单向，并且不会重复访问某个节点，否则就会陷入无限循环。

因此我们创建一个数组、一个集合和一个计数器：

   let res = [];                // to store the result
   let visited = new Set();     // to store visited nodes
   let count = 0;               // safety check to ensure all nodes are visited

接下来的步骤是：
步骤 1> 遍历队列，
步骤 2> 弹出一个节点，
步骤 3> 通过将该节点设置为已访问并将其添加到结果中来处理该节点，
步骤 4> 访问当前节点的所有子节点并将其入度减少 1，
步骤 5> 增加计数，
步骤 6> 重复步骤 1 - 5，直到队列为空。

while(queue.length>0){
      // pop a node from queue
      let node = queue.shift();

      // check if it's visited, if it's the return 0
      if(visited.has(node)) return 0;

      // add node to visited set
      visited.push(node);

      // add node to result
      res.push(node);

      //loop over all the nodes require current node as a prerequisite
      for(let n of graph[node]){

          // since current node is processed, decrease the indegree of node "n" by 1
          indegree[n]--;

          // if node "n" indegree equals 0, add it to the queue so that it can be processed
         if(indegree[n] == 0) queue.push(n);
      }

      // incremenet count by 1
      count++;
}

让我们以动画形式查看上述步骤。如果可以的话，请在另一个选项卡中打开 gif 动图，并将每个步骤与上面的代码进行比较。

把它们放在一起：

 var topologyOrder = function(numCourses,prerequisites){

       let graph = new Array(numCourses);

       let indegree = new Array(numCourses);

       for(let i=0;i<numCourses;i++){
           graph[i] = []; 
       }

       for(let prerequisite of prerequisites){
           let from = prerequisite[1];
           let to = prerequisite[0];
           graph[from].push(to);
           indegree[to]++;
       }

       let queue = [];

       for(let i=0;i<indegree.length;i++){
            if(indegree[i] == 0){
               queue.push(i);
            }
       }

       if(queue.length == 0) return 0;

       let res = [];                
       let visited = new Set();     
       let count = 0;

       while(queue.length>0){
             let node = queue.shift();
             if(visited.has(node)) return 0;
             visited.add(node);
             res.push(node);
             for(let n of graph[node]){
                  indegree[n]--;
                  if(indegree[n] == 0) queue.push(n);
             }
             count++;
      }

      return count == numCourses ? res : 0;
}

如果您读到这里，非常感谢 :) 我希望您喜欢我的文章。

如果我在某个地方搞砸了或者没有解释清楚，请发表评论。

github：https://github.com/AKHILP96/Data-Structures-and-Algorithms/blob/master/Algorithm/TopologicalSort.js

鏂囩珷鏉ユ簮锛�https://dev.to/akhilpokle/topological-sort-solving-google-interview-question-cb