设计 Trie 树，解决 Uber 面试题

我偶然看到了一篇关于他如何通过一道谜题在谷歌找到工作的文章。这篇文章主要讲的是他用来解决这个难题的数据结构。

在本文中，我们将介绍：
1> 什么是 Tries 树。2
> 为什么以及如何使用它们。3
> 如何在 javascript 中实现一个简单的 Trie。

所以他直接用 Trie/后缀树来解决这个难题，

什么是 Trie？

尝试是一种基于树的数据结构，用于有效地存储字符串。

它们是如何使用的？

假设您的任务是存储美国所有城市的名称。

最简单的方法是获取所有城市名称并将其存储在数组中，但由于您是一名忍者开发人员，您会注意到一种模式，它可能有助于减少存储所有城市名称所需的总空间。

例如：以下是名称中带有前缀“New”的所有城市的列表。

 "New Albany"                          "New Bedford"
 "New Bern"                            "New Braunfels"
 "New Britain"                         "New Kensington"
 "New London"                          "New Madrid"
 "New Market"                          "New Martinsville"
 "New Mexico"                          "New Milford"
 "New Orleans"                         "New Paltz"
 "New Philadelphia"                    "New Rochelle"
 "New Smyrna Beach"                    "New Ulm"
 "New Windsor"                         "New York"
 "New York City"                       "New Brunswick"
 "New Castle"                          "New Glarus"
 "New Hampshire"                       "New Harmony"
 "New Haven"                           "New Hope"
 "New Iberia"                          "New Jersey"

那么，与其每次都重复“新”，不如压缩它怎么样？

由于“New”是一个常见的前缀，我们可以从所有单词中删除“New”
，并创建一个数据结构，自动将“New”附加到上面提到的城市，例如：例如：对于 4 个城市，它看起来像：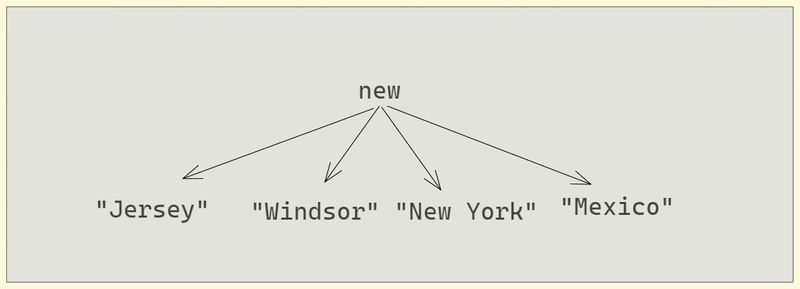

但更进一步怎么样？
由于“New Madrid”、“New Market”和“New Martinsville”都包含“New Ma”，让我们进一步压缩字符串。

对每个城市都进行这样的操作，我们得到如下结果：

在这里玩得开心

具有相同前缀的城市被分组在一起，这有助于减少空间。

还有更多!!!
使用 tries 可以使搜索变得更快，怎么做？

让我们模拟一个同时存在于 trie 和数组中的搜索：搜索速度非常快，因为我们不需要遍历数组，而是在 6 个刻度内就能得到结果。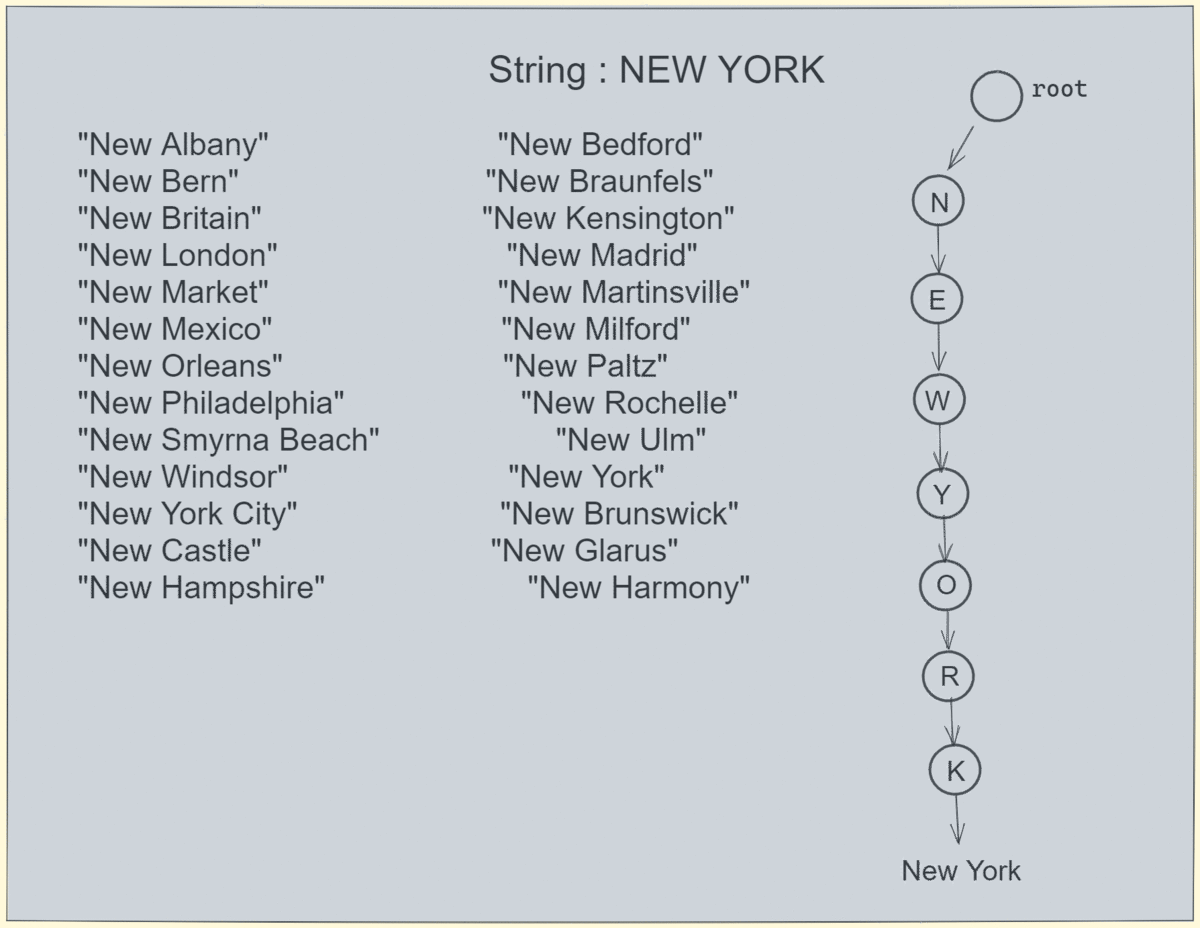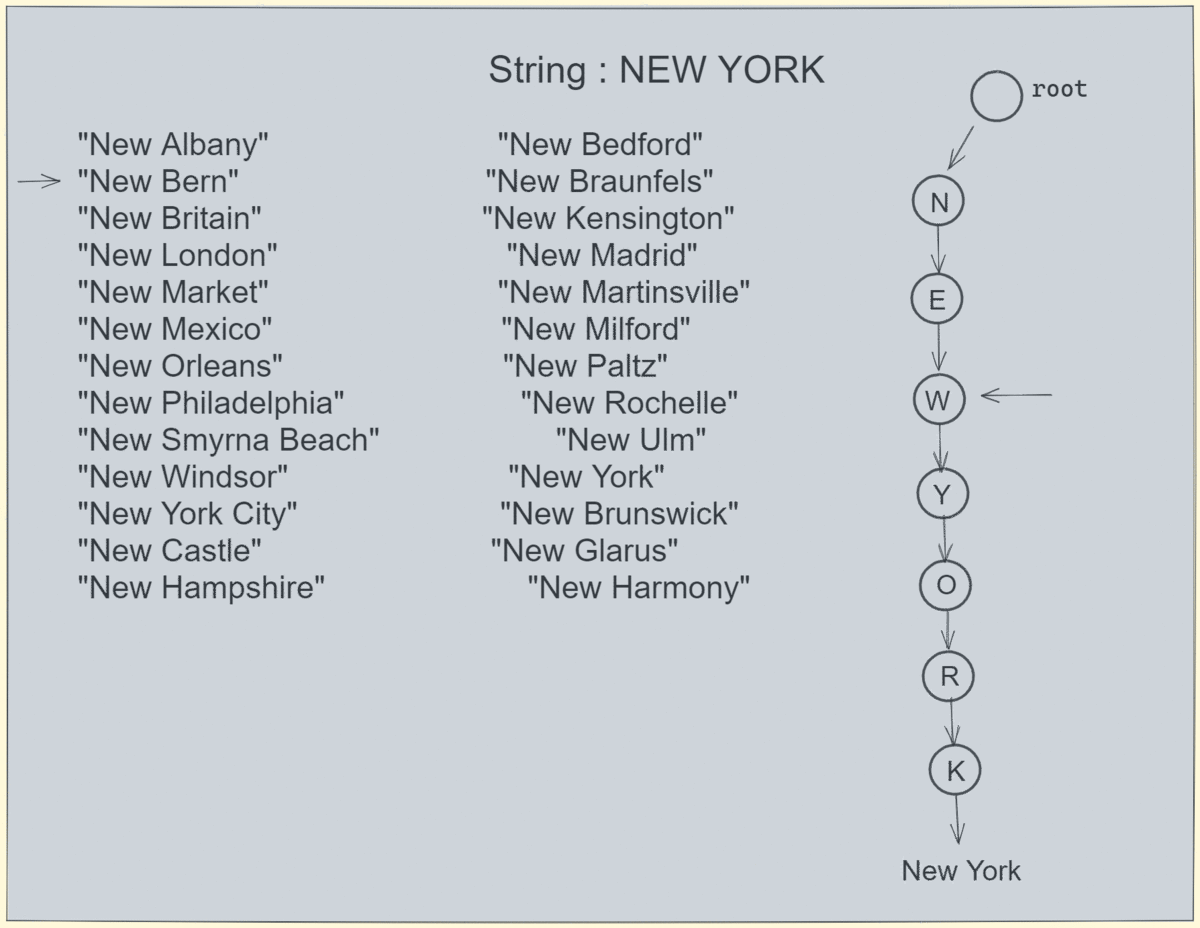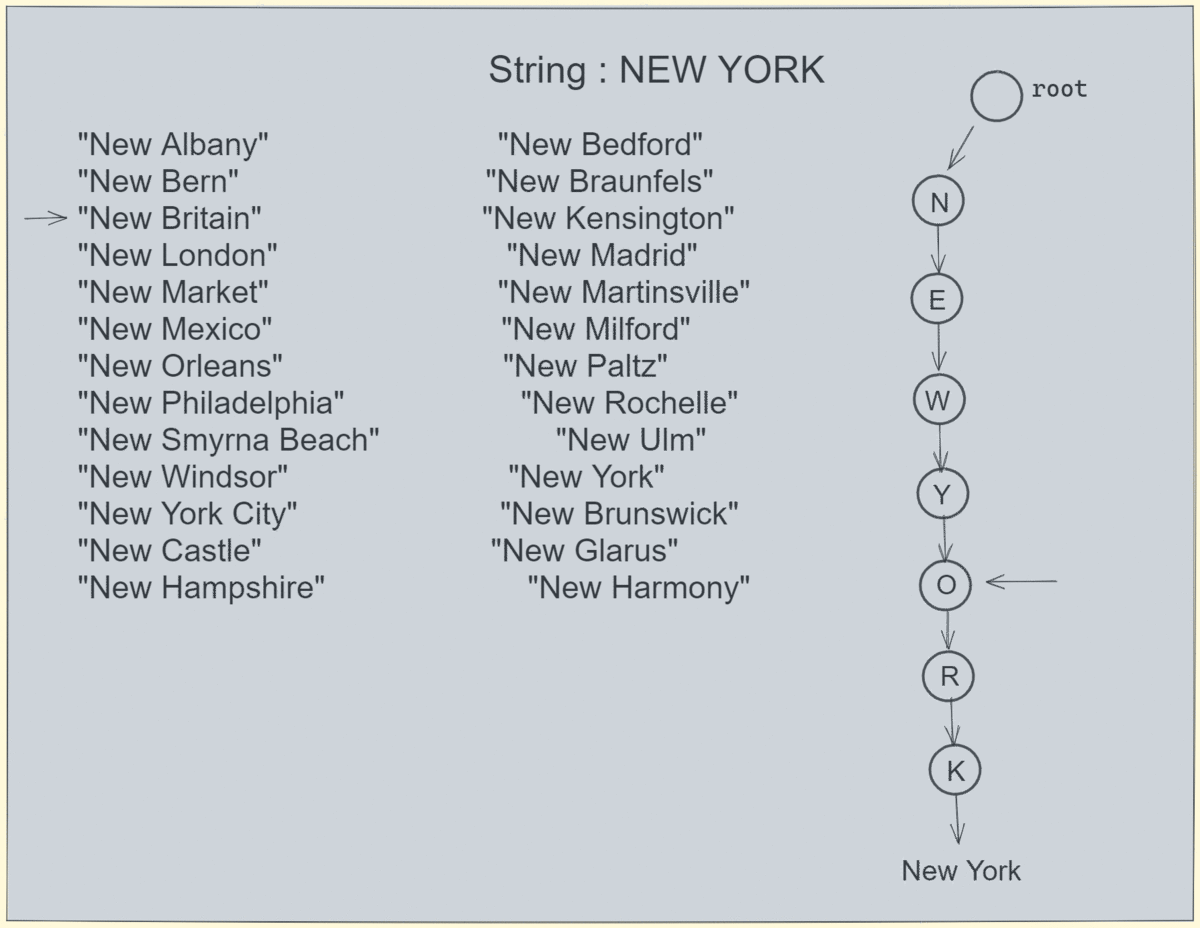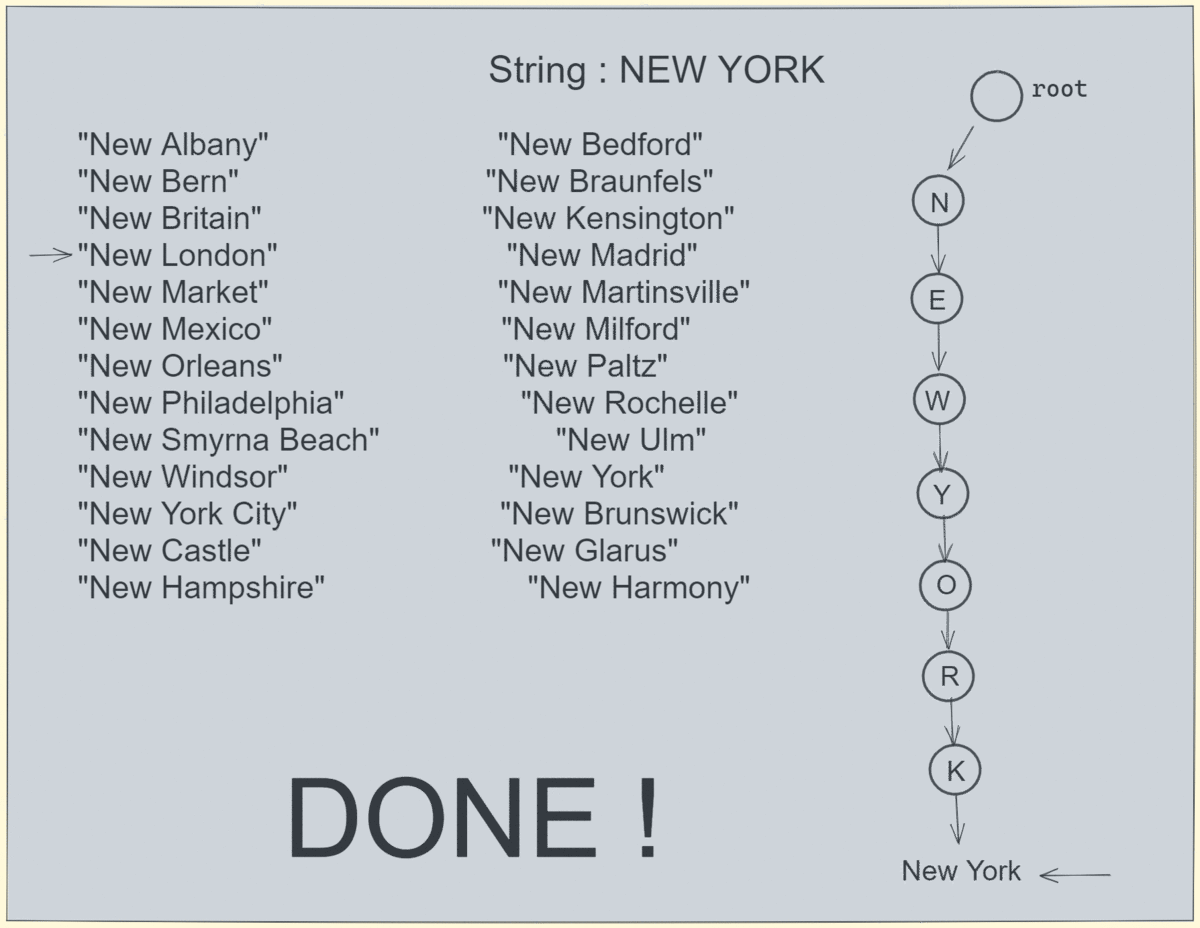

搜索在 trie 和数组中不存在的字符串：在 4 个刻度内，我们可以确定搜索字符串是否存在。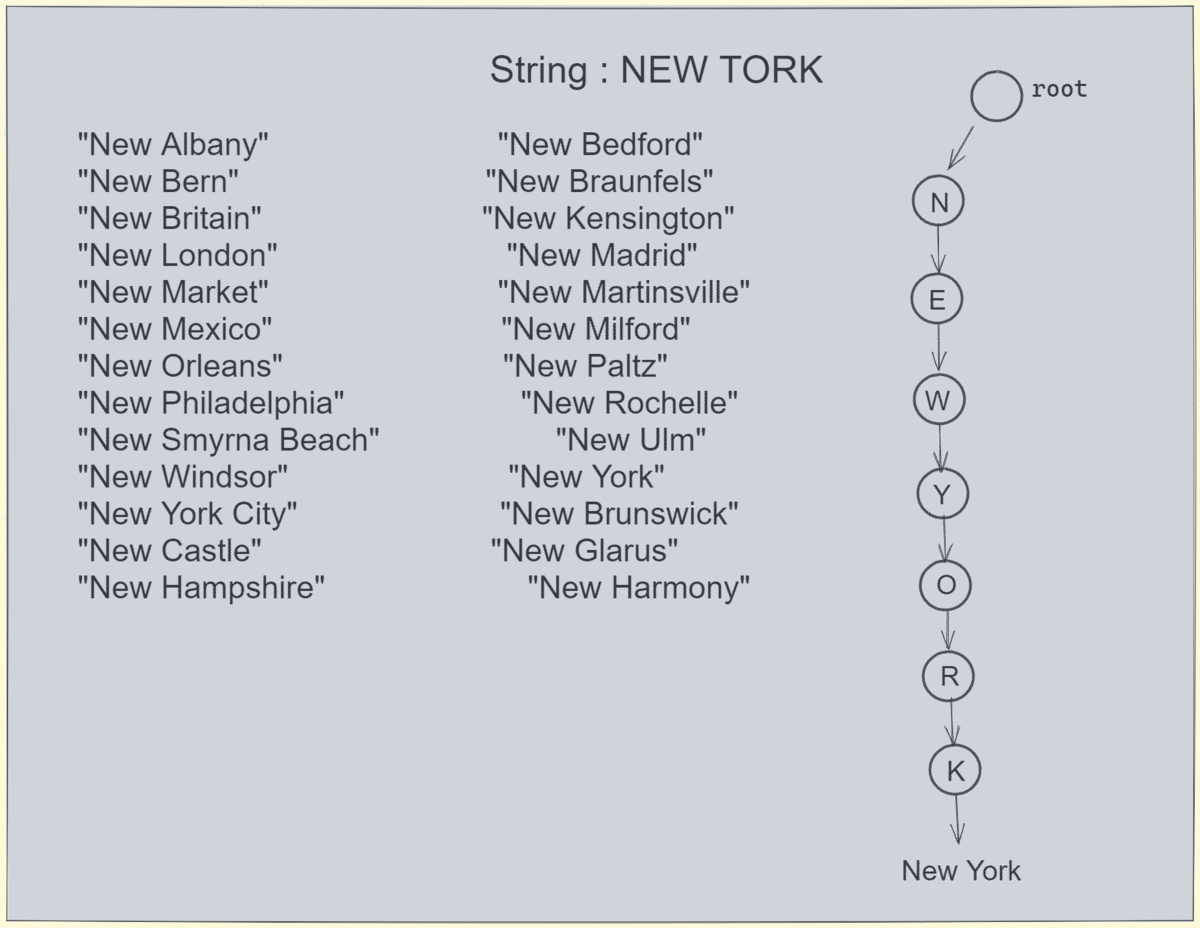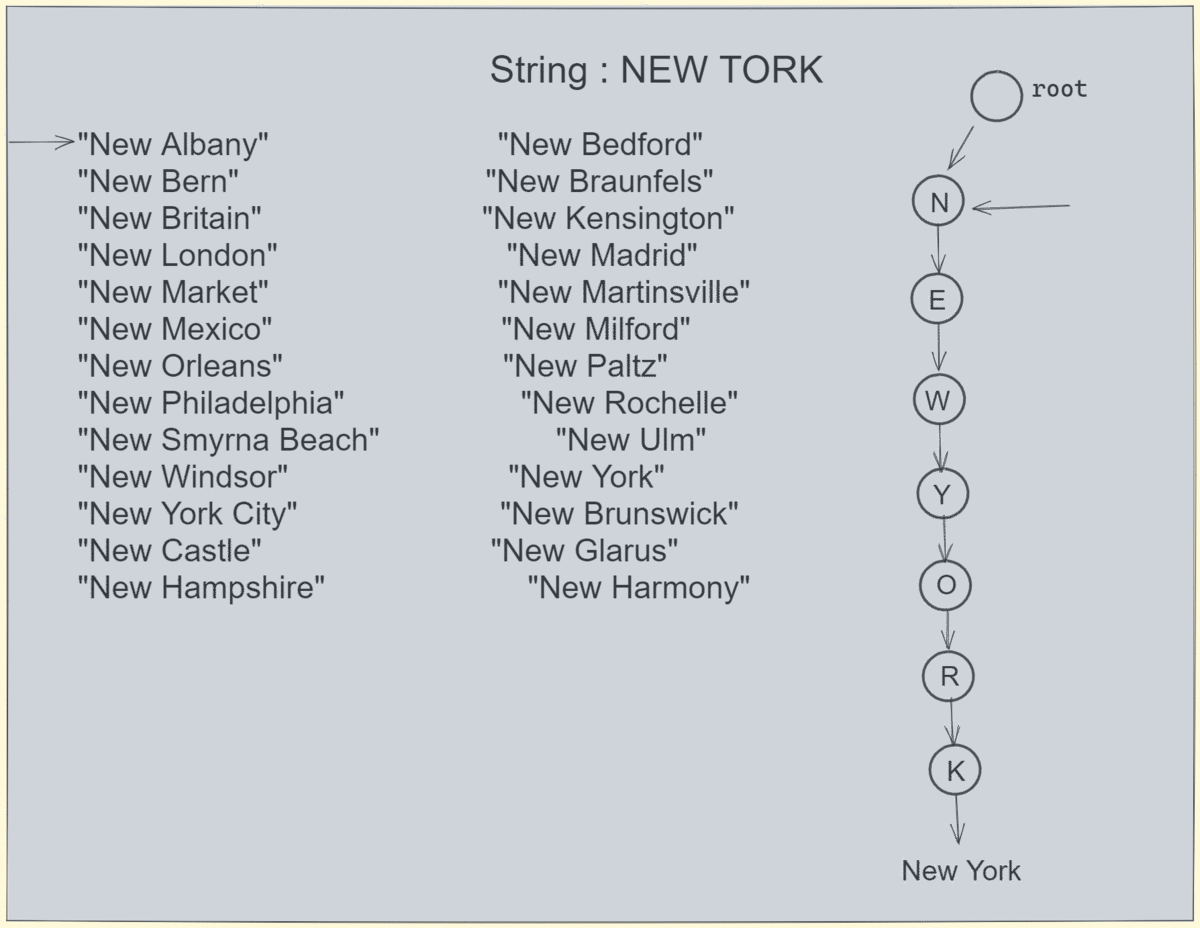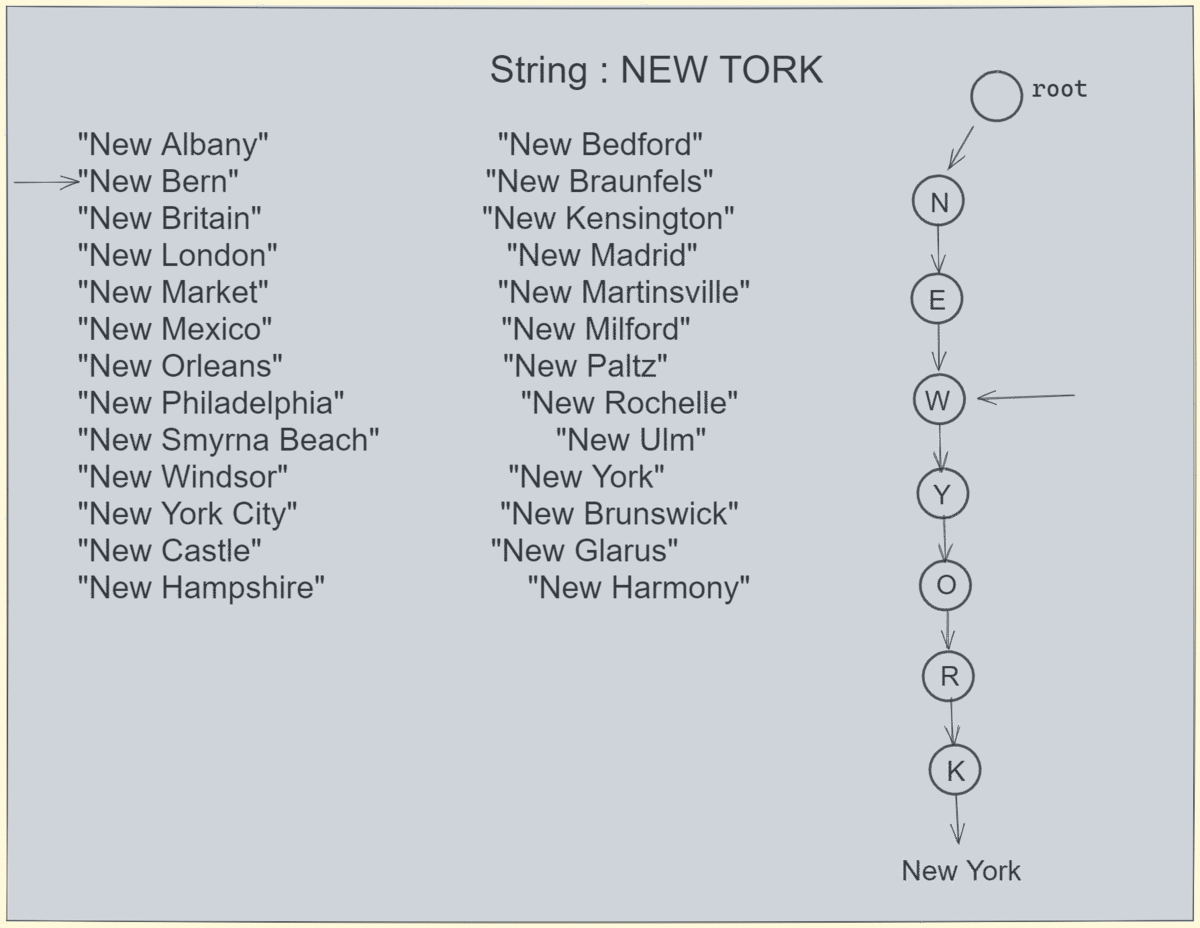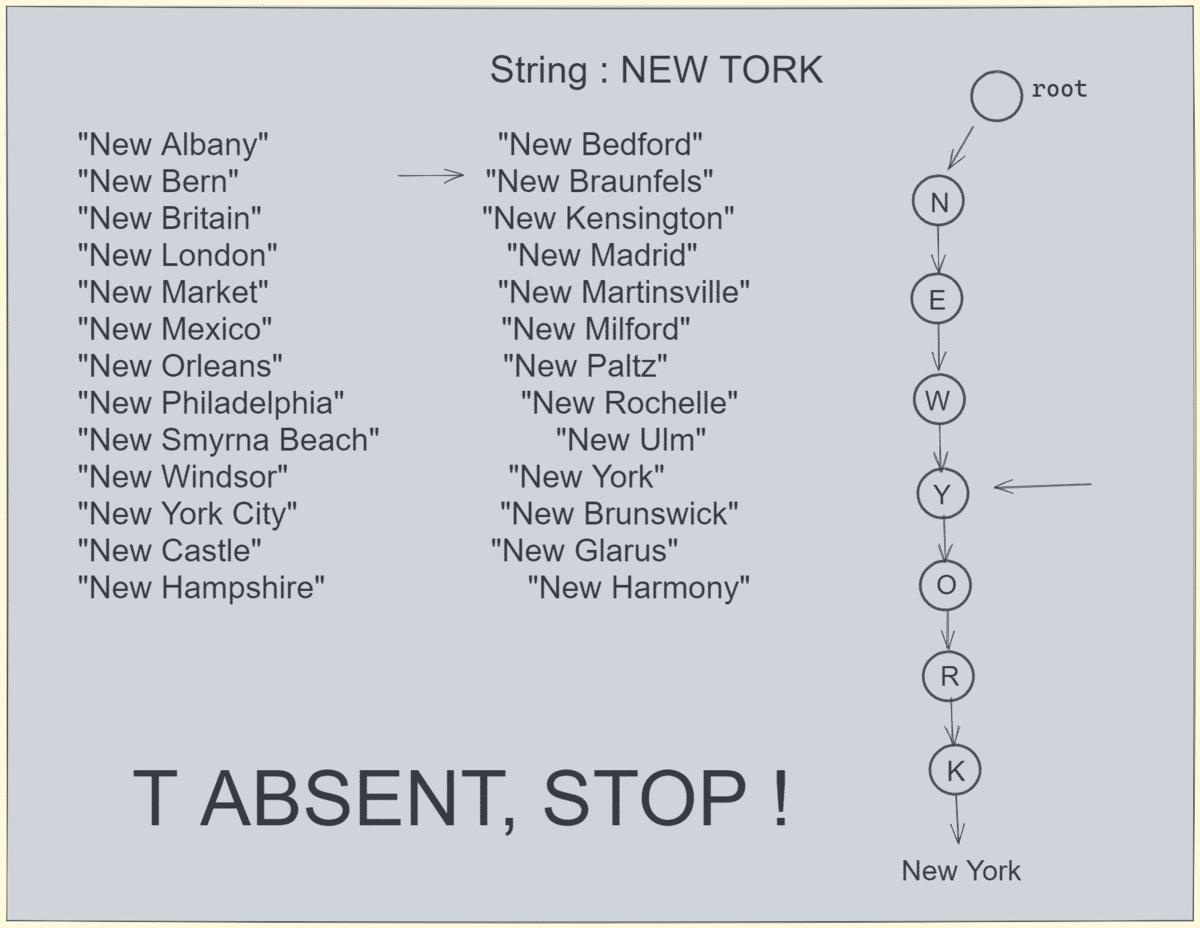

应用：

Trie 在许多地方都有使用，例如自动完成功能（我们将在下一篇博客中构建此功能）、数据分析、Gnome 分析、拼写检查器等。

现在我们知道了什么是 trie，以及它为什么有用，让我们来构建一个吧！

构建 Trie

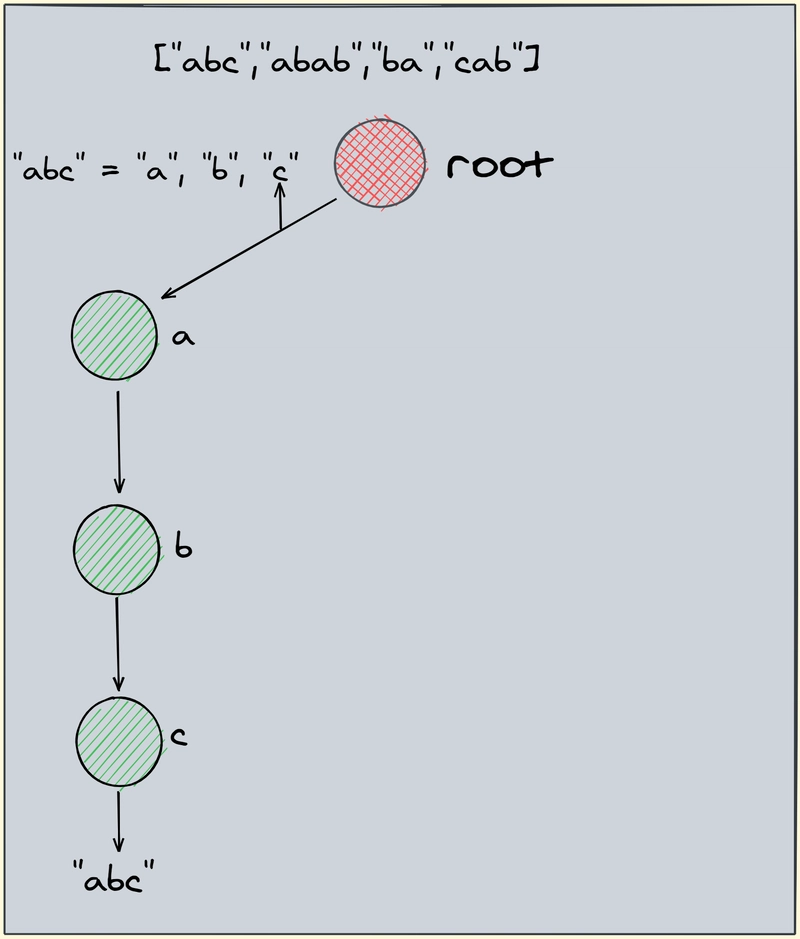
我们将为以下项构建 Trie：['abc','abab','babc','cab']

为了提高效率，我们将使用对象构建 Trie 以利用 O（1）查找。

步骤 1

由于我们基本上是在构建一棵树，所以我们需要一个根，对于 Trie 来说，根将是空的，但会存储有关其子对象的信息。

class Trie{
    constructor(){
         this.root = {}
    }
}

第 2 步：

现在让我们遍历数组 ['abc','abab','ba','cab'] 中的每个字符串并创建一棵树。

首先是“abc”：
我们检查“a”是否存在于树中，由于根节点为空，因此不存在，因此将“a”添加到字典树中，然后是“b”，最后是“c”。现在，由于我们已经到达字典树的末尾，我们存储单词“abc”，以表明“是”，“abc”是一个有效的单词。

我们最终到达这里：

第二个“abab”。
我们重复相同的过程，检查“a”是否存在，如果存在，我们就不会创建新节点，而是转到“a”节点。然后检查“b”是否存在，如果“b”连接到“a”，那么转到“b”节点。再次检查“a”是否存在，如果“a”节点没有连接到“b”，我们创建一个新的“a”节点，并将其连接到“b”，并继续重复该操作。

因此，将字符串插入 Trie 可以归结为 3 个基本步骤：

1> 如果字符未连接到节点，则创建一个新字符并遍历。2
> 如果字符已连接到节点，则遍历该节点。3
> 如果这是字符串的末尾，则将字符串添加到当前子树的叶子节点。

可视化：

让我们将其翻译成代码：

  insert(word) {
    let node = this.root;                            
    for (let c of word) {
      if (node[c] == null) node[c] = {};             //if {c} not present, create one
      node = node[c];                                // travese{c} 
    }
    node.isWord = true;                              // add word.
  }

因此，对于每个字符串，从根开始遍历。
对于每个字符 c，检查是否创建了对象，如果没有，则创建一个并遍历它。
最后，我们将“abc”设置为 true，表示“是的，包含“abc”的字符串是可能的。”

因此对于 ["abc","abab"] 我们实际的 trie 将如下所示：

let root = {
  "a":{
    "b":{
      "c":{
        isWord:true
      },
      isWord:false,
      "a":{
        "b":{
          "isWord":true
        },
        isWord:false
      },
      isWord:false
    },
    isWord:false
  },
  isWord: false
}

console.log(root.a);
console.log(root.a.b);
console.log(root.a.b.c);
console.log(root.a.b.c.isWord);
console.log(root.a.b.a);
console.log(root.a.b.a.b);
console.log(root.a.b.a.b.isWord);
console.log(root.a.b.isWord);
console.log(root.a.b.f == null);

现在让我们创建一个函数来遍历它，这类似于插入：

 traverse(word) {
    let node = this.root;
    for (let c of word) {
      node = node[c];
      if (node == null) return null;
    }
    return node;
  }

为了搜索，我们遍历字符串，最后检查“isWord”是否设置为 true ：

  search(word) {
    const node = this.traverse(word);
    return node != null && node.isWord === true;
  }

把它们放在一起：

class Trie {
  constructor() {
    this.root = {};
  }

  insert(word) {
    let node = this.root;
    for (let c of word) {
      if (node[c] == null) node[c] = {};
      node = node[c];
    }
    node.isWord = true;
  }

  traverse(word) {
    let node = this.root;
    for (let c of word) {
      node = node[c];
      if (node == null) return null;
    }
    return node;
  }

  search(word) {
    const node = this.traverse(word);
    return node != null && node.isWord === true;
  }
}

我认为这篇文章已经够长了，下一篇文章我将写如何基于 Trie 创建搜索自动完成功能。

github：https://github.com/AKHILP96/Data-Structures-and-Algorithms/blob/master/DataStructures/Trie.js

鏂囩珷鏉ユ簮锛�https://dev.to/akhilpokle/design-trie-solving-an-uber-interview-question-1k4i