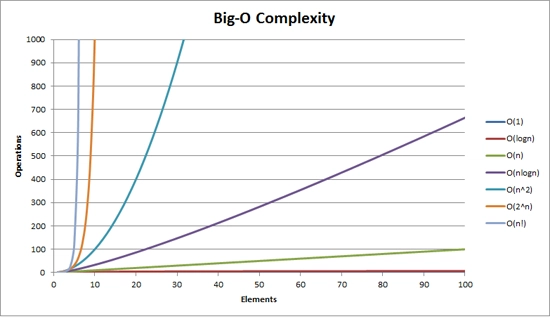
Big O，代码效率分析

在本文中，我将尽力向您介绍算法复杂度，以及如何使用大 O 符号粗略地测量它。您也可以访问chirila.dev/writing/cfa查看原文。

为什么测量代码效率很重要

首先，或许它之所以如此重要的一个原因在于，我们想要推断当前代码如何影响我们的程序。我们可以在较小的规模上测试代码，但如何预测代码在更大规模上的运行方式，以及我们编写的代码如何解决特定规模的问题呢？

第二个原因是，理解我们在设计或实现算法时编写的代码将如何影响当前的问题。你可以根据某些数据结构或实现细节如何影响程序的最终时间复杂度来做出决策。

我们为什么要关心

通常，人们会给出一个理由来解释为什么你不应该关心它，那就是计算机的速度越来越快，计算速度也越来越快。但另一方面，计算的数据量也越来越大，以至于谷歌在 2016 年宣布他们正在处理130.000.000.000.000 （130 万亿）个网页，而他们在 2013 年的报告中只处理了大约 30.000.000.000.000（30 万亿）个网页。虽然计算机速度越来越快是毋庸置疑的事实，但我们可以看到，我们处理的数据量越来越庞大，因此即使在今天，仅仅编写一个覆盖整个数据集的简单算法也是不够的。

预先要求

为了理解本文，建议您先了解以下一些预览知识：

对算法的基本理解
对计算机科学基础知识有基本了解
对数据结构有基本的了解

代码分析

现在我们了解了编写高效代码的重要性，让我们来讨论一下是什么让我们的代码高效以及如何衡量算法的复杂性。

我们可以通过以下方式衡量算法的复杂度：

时间（持续时间）
空间（内存）

考虑到这一点，一个大问题随之而来：我们如何概括和抽象这些测量指标。如果我们谈论时间复杂度，那么我们如何测量程序执行一段代码所需的时间呢？我们当然可以使用计时器来计算，这是最直观的方法。在Node中，我们可以简单地记录执行前后的时间，然后相减：

function average(nums) {
  let total = 0;
  for(let i = 0; i < nums.length; i++) {
    total += nums[i];
  }
  return total / nums.length;
};

const start = new Date();
average([23, 51, 88, 49, 90, 7, 64, 77, 12, 8, 96]);
const end = new Date();

console.log(`Execution time: ${end - start}ms`);

采用这种特殊方式会导致测量结果不一致：

执行时间，因算法而异
执行时间因实现而异
执行时间因系统/计算机而异
执行时间，在更大范围内是不可预测的

为了一致地测量算法，我们需要一个更好的替代方案，它可以：

计算我们执行的操作数量，而不必担心实现细节
关注时间和空间复杂度如何扩展
根据输入的大小和采取的步骤数来衡量算法

业务增长

让我们看一个代码示例，它将遍历元素列表并返回列表中是否存在元素：

function find(list, element) {
  for(let i = 0; i < list.length; i++) {
    if(list[i] === element) return true;
  }
  return false
};

在这种情况下，我们代码的时间复杂度是多少？嗯，这取决于你有多幸运。可能是列表中的第一个元素是我们的元素，在这种情况下它只循环一次，然后就完成了，这被称为最佳情况。但也可能是我们的元素不在列表中，在这种情况下我们必须遍历整个列表并返回false，这是最坏的情况。我们还可以对这段代码运行多个示例，看看它经历了多少次迭代，这将给我们平均情况，平均而言，我们可能会查看列表的一半来找到我们的元素。

渐近符号

渐近符号是用来表示算法复杂性的数学工具。常用的符号有三种：

Big Omega (Ω) Notation，给出算法的下限（最佳情况）
Big Theta (Θ) Notation，给出算法的精确界限（平均情况）
Big Oh (O) Notation，给出算法的上限（最坏情况）

有时查看平均情况会很有用，可以让您大致了解算法在长期内的表现，但是当我们谈论代码分析时，我们通常谈论最坏情况，因为它通常定义了我们所追求的瓶颈。

大 O 符号

让我们看一下之前的示例，该示例计算给定数字列表的平均值，具体来说是第3行：

function average(nums) {
  let total = 0;
  for(let i = 0; i < nums.length; i++) {
    total += nums[i];
  }
  return total / nums.length;
};

average([23, 51, 88]);

我们马上注意到一个从起点i = 0到的循环i < nums.length，这意味着这段代码的时间复杂度将是给定输入的大小nums，在本例中，其长度为3 （nums列表中的元素）。我们可以将输入名称概括为n。因此，我们可以说平均函数的复杂度为O(3n)，此外，我们可以删除任何系数和常数，剩下的复杂度为O(n)。

此时您可能想知道我们如何能够去掉 3；这只是我们做出的一个简化，这是可能的，因为 Big O 只对我们的算法的性能如何随着输入的大小而变化感兴趣。

简化

让我们看一些简化的例子，以便更好地理解如何简化我们的符号。

O(6 * n) = O(n)
O(14n) = O(14 * n) = O(n)
O(3891n) = O(3891 * n) = O(n)
O(n / 4) = O(¼ * n) = O(n)
O(3n * n * 322) = O(n * n) = O(n ² )
O(n² ⁺ 2n+9)= O( ^n² )
O(800 + n + n ³ + n ² ) = O(n ³ )
O(4n ¹² + 2 ⁿ ) = O(2 ⁿ )
O(441) = O(1)

现在我们已经看到了一些例子，我们可以继续定义一些规则：

乘法定律

与语句一起使用nested>当 Big O 是多个项的乘积时，我们可以删除任何系数和常数

加法定律

sequential与语句一起使用>当 Big O 是多个项的总和时，我们可以保留最大的项，并删除其余项

时间复杂度分析示例

为了更好地理解如何分析代码的时间复杂度并简化符号，让我们看一些简单的例子。

// We have 2 separate loops
// O(3n + 3n) = O(n) -> addition, we keep the largest term
function exampleOne(n) {
  for(let i = 0; i < n.length; i++) {
    // code
  }
  for(let j = n.length - 1; j > 0; i--) {
    // code
  }
};
// calling the function with [1, 2, 3] -> list of length 3
exampleOne([1, 2, 3])

// We have 2 separate loops, one of them being a nested loop
// O(5n * 5n + n / 2) = O(n² + n) = O(n²) -> addition, we keep the largest term
function exampleTwo(n) {
  for(let i = 0; i < n.length; i++) {
    for(let j = 0; j < n.length; j++) {
      // code
    }
  }
  for(let k = n.length / 2; k > 0; k--) {
    // code
  }
};
// calling the function with [5, 6, 7, 8, 9] -> list of length 5
exampleTwo([5, 6, 7, 8, 9])

// First outer loop, iterates a constant number of times (100), and has a nested loop
// Second loop, iterates a constant number of times (4350)
// O(100 * 4n + 4350) = O(n) -> addition, we keep the largest term
function exampleThree(n) {
  for(let i = 0; i < 100; i++) {
    for(let j = 0; j < n.length; j++) {
      // code
    }
  }
  for(let k = 0; k < 4350; k++) {
    // code
  }
};
// calling the function with [2, 4, 6, 8] -> list of length 4
exampleThree([2, 4, 6, 8])

空间复杂度分析示例

到目前为止，我们只讨论了时间，但根据系统的规格，空间也同样重要。我们的内存可能有限，因此我们必须在时间复杂度上做出一些权衡，以获得更好的空间复杂度。

// 3 variables created that are not dependent of the input size
// O(3) = O(1) -> simplification of a constant term
function average(list) {
  // declaring a variable 'total'
  let total = 0;
  // declaring a variable 'i' once
  for(let i = 0; i < list.length; i++) {
    /**
    Even though we create this variable every loop
    at the end of each iteration it will be disposed
    so we only ever have one variable
    */
    const current = list[i]
    total += current;
  }
  return total / list.length;
};

// 3 variables created, one grows with the input size
// O(2 + n) = O(n) -> addition, we keep the largest term
function reverse(list) {
  // variable grows with the input size
  const reversedList = [];

  for(let i = list.length - 1; i >= 0; i--) {
    const current = list[i];
    // pushing each element in the list in the 'reversedList' thus growing it's size
    reversedList.push(current);
  }
}

复杂性类

我们将按照从性能最高到性能最低的升序顺序介绍一组复杂性类别。

让我们看看这些类别如何随着输入大小而扩展；

班级	n=10	n=100	n=1000	n=1000000
O(1)	1	1	1	1
O（log n）	1	2	3	6
在）	10	100	1000	1000000
O(n log(n))	10	200	3000	6000000
O(n²)	100	10000	1000000	1000000000000
O(2ⁿ)	1024	1267650600228229401496703205376	玩得开心！	玩得开心！

常数——O(1)

所需的时间或步骤与输入大小无关
可以有循环或递归函数，只要迭代次数或调用次数与输入大小无关

当我们想要确定常数时间时，我们通常会寻找那些不随输入大小增长/缩放的操作，通常是那些不会在输入大小上迭代的代码。我们认为可以以常数时间运行的操作包括：算术运算、访问数组索引、哈希表查找、将节点插入链表。

// Time: O(1) -> does not depend on the input size
// Space: O(1) -> does not grow with the input
function isEven(n) {
  let result;
  if(n % 2) {
    result = false;
  } else {
    result = true;
  }
  return result;
}

// Time: O(1)
// Space: O(1)
function sumFirstAndLast(list) {
  // accessing array index and getting it's length is a constant operation
  const result = list[0] + list[list.length - 1];
  return result;
}

对数 – O(log(n))

所需的时间或步骤的数量随着输入大小的对数增长

为了更好地理解这句话的意思，我们需要先了解什么是对数。简而言之，alogarithm是 an 的反义词exponent。如果指数是乘，那么对数是除。

指数

2 ⁴ = 16 – 2 * 2 * 2 * 2
我们说 2 的 4 次方是 16

对数

log ₂ 16 = 4 – 16 / 2 = 8 / 2 = 4 / 2 = 2 / 2 = 1
我们计算一下除以2的次数（4 次）， 2就是我们的基数
我们说 16 的 2 进制对数是 4

一些具有对数复杂度的算法是二分搜索和二分搜索

// Time: O(log(n)) -> each iteration we divide by 2
// Space: O(1)
function countDownStep(n, step = 2) {
  for(let i = n; i > 0; i /= step) {
    console.log(i);
  }
}

// Binary search of a list
// Time: O(log(n)) -> each iteration we divide our list by 2
// Space: O(1)
function indexOf(list, element) {
  let start = 0;
  let end = list.length - 1;

  while(start <= end) {
    let mid = Math.floor((start + end) / 2);
    // if element is at the middle we return it's index
    if(list[mid] === element) return mid;
    // going either right or left of the list
    if(list[mid] < element) {
      start = mid + 1;
    } else {
      end = mid - 1;
    }       
  }
  return -1;
}

线性 – O（n）

所需的时间或步骤取决于输入的大小
迭代循环和递归函数

此时我们已经看到了很多线性迭代复杂性，所以让我们看一些例子，其中我将包括一个迭代和递归线性复杂性的例子（如果你不熟悉递归，我建议你研究它，会在某个时候写一篇关于它的文章并在这里链接它）。

// Iterative factorial
// Time: O(n) -> iterating n times
// Space: O(1) 
function iterFactorial(n) {
  let product = 1;
  for(let i = 1; i <= n; i++) {
    product *= i;
  }
  return product;
}

// Recursive factorial
// Time: O(n) -> number of function calls is dependent of n
// Space: O(n) -> there are always n function calls in our call stack
function recurFactorial(n) {
  // base case
  if(n <= 1) return 1;

  return n * recurFactorial(n - 1);
}

如果你对这两个函数进行计时，你可能会注意到，由于函数调用的原因，递归函数的运行速度比迭代函数慢。你可以使用memoization策略来优化它，但我会在另一篇文章中讨论这个问题。

线性对数 – O(n log(n))

所需的时间或步骤取决于输入的大小，输入的大小呈对数增长
嵌套在日志复杂度循环中的顺序循环

线性对数复杂度也称为对数线性或n log n，这种特殊的复杂度大于O(n)但小于O(n² ⁾。许多实际算法都是线性对数的，最常用的是归并排序和快速排序。

// Time: O(n log(n)) -> sequential loop (slice method), nested into log loop
// Space: O(1)
function iterPrintHalf(str) {
  for(let i = str.length; i >= 1; i /= 2) {
    const result = str.slice(0, i);
    console.log(result);
  }
}

// Time: O(n log(n)) -> sequential loop (slice method), into log recursive call
// Space: O(n) -> there are always n size function calls in our call stack
function recurPrintHalf(str) {
  console.log(str);
  if(str.length <= 1) return;

  const mid = Math.floor(str.length / 2);
  const result = str.slice(0, mid);

  return recurPrintHalf(result);
}

多项式 – O(n ^c )

n为输入的大小，c为常数，其中c > 1
通常是多个嵌套循环或递归调用
包括二次O(n ² )、三次O(n ³ )

大多数多项式算法都是二次的，包括冒泡排序、插入排序、选择排序、遍历二维数组

// Time: O(n²) -> 2 nested loops
// Space: O(1)
function bubbleSort(list) {
  for (let i = 0; i < list.length; i++) {
    let temp1 = list[i];

    for (let j = i + 1; j < list.length; j++) {
      let temp2 = list[j];

      if(temp1 > temp2) {
        // swap
        list[i] = temp1;
        list[j] = temp2;
        // update
        temp1 = list[i];
        temp2 = list[j];
      }
    }
  }
  return list;
}

指数 – O(c ⁿ )

n为输入的大小，c为常数，其中c > 1
递归函数，对每个大小的输入进行多次调用

许多重要问题本质上都是指数级的，但由于成本可能很高，我们往往会考虑更近似的解决方案，因为它们能提供更优的时间复杂度。一些指数级算法包括汉诺塔算法、递归斐波那契算法。

// Time: O(2ⁿ) -> two recursive calls are made for each input
// Space: O(n) -> we only have n calls on the call stack
function fibonacci(n) {
  if(n === 0) return 0;
  if(n === 1) return 1;

  return fibonacci(n - 1) + fibonacci(n - 2);
}

这个递归函数可以通过使用memoization策略来优化。

阶乘 – O(n!)

递归函数，每次调用都取决于输入的大小

指数和阶乘的主要区别在于，指数算法中我们进行常数次递归调用，而阶乘算法中我们进行n次递归调用。流行的阶乘算法包括旅行商算法、排列算法。

// Time: O(n!) -> n recursive calls are made based on the size of the input
// Space: O(n) -> we only have n calls on the call stack
function trivialExample(n) {
  if(n === 1) return 1;
  // code

  for(let i = 0; i < n; i++) {
    trivialExample(n);
  }
}

// Time: O(n!) -> n recursive calls are made based on the size of the input
// Space: O(n) -> we only have n calls on the call stack
function permutations(string, char = "") {
  if(string.length <= 1) return [char + string];

  return Array.from(string).reduce((result, char, idx) => {
    const reminder = string.slice(0, idx) + string.slice(idx + 1);
    result = result.concat(permutations(reminder, char));
    return result;
  }, []);
}

结论

我们讨论了编写高效代码的重要性，以及可以采取哪些策略来衡量代码效率。我们介绍了大 O 符号作为分析算法复杂度的通用方法，并简要介绍了另外两种渐近符号。然后，我们使用大 O 符号分析了一些代码，讨论了最常用的复杂度类别以及它们如何随输入规模的变化而变化，并举例说明如何更好地形象化和理解我们通常分析代码的方式。

资源

文章来源：https://dev.to/kerosz/big-o-code-efficiency-analysis-phk

Big O，代码效率分析

Big O，代码效率分析

为什么测量代码效率很重要

我们为什么要关心

预先要求

代码分析

业务增长

渐近符号

大 O 符号

简化

时间复杂度分析示例

空间复杂度分析示例

复杂性类

常数——O(1)

对数 – O(log(n))

线性 – O（n）

线性对数 – O(n log(n))

多项式 – O(n c )

指数 – O(c n )

阶乘 – O(n!)

结论

资源

多项式 – O(n ^c )

指数 – O(c ⁿ )