面向 JavaScript 开发人员的实用大 O 符号

大 O 符号是我们在接受某种正规教育（例如大学）时通常会学到的东西之一，否则，我们日常的实际方面往往会超越它，并使它成为一个完全次要的术语，我们可以没有它——而你们中的许多人都是这样的！

话虽如此，我仍然相信从高层次理解这种符号是有好处的。快速理解算法的性能影响不仅有用，而且非常实用。

那么让我们快速了解一下什么是 Big O 符号以及您到底应该注意什么。

什么是大 O 符号？

Big O 符号只不过是一种描述算法的复杂性和性能的数学方式。

我拒绝深入探讨如何计算精确表达式，因为说实话，你可能永远都不需要它。相反，你只需要它的简化版本，它能让你了解，当算法需要处理的值数量增加时，其复杂度会增长得有多快。

这么说吧：大 O 符号是一种图形化表示算法复杂度增长速度的方式，当它所需的数据点数量趋近于无穷大时。或者，它也可以用来比较同一领域内的两个算法，大 O 符号较低的算法通常更好，至少在性能方面是这样。

我知道，这听起来不太简单，但让我告诉你我的意思：

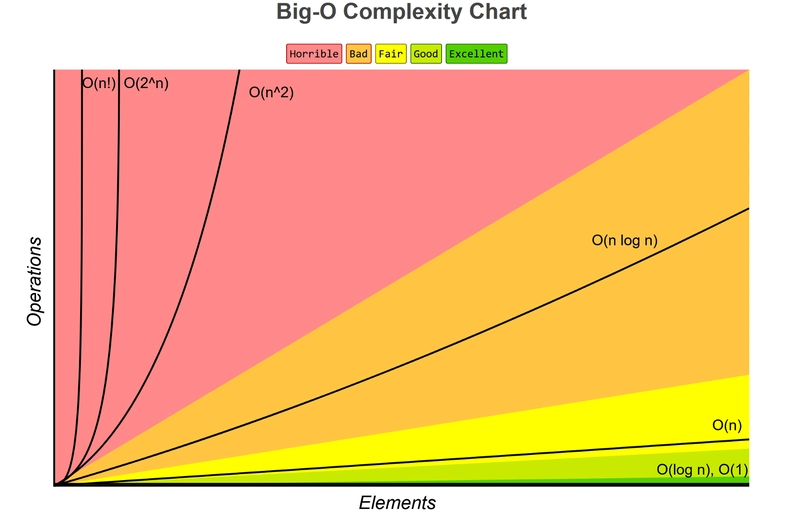
查看上图并将 Y 轴视为复杂性，而 X 轴是算法将处理的元素数量（此处“元素”可以是任何东西，从变量数量到潜在的不同值，甚至可能是需要执行的指令数量，我们将看到一些示例）。

我不会在这里逐一讨论每个选项，因为如果你到现在还没有使用过 BigO，那么理解 O(n!)、O(nlogn)、O(n)、O(logn) 和 O(1) 的含义对你来说已经很有帮助了。其余的选项介于 O(n!)、O(nlogn)、O(n)、O(logn) 和 O(1) 之间，读完本文后你应该能够判断它们是否适合你。

在！）

让我们从最坏的情况开始，即 O(n!) 情况，即上图中的黑线。

有时你无法避免它，但如果可以的话，你应该尽量远离这些类型的算法，因为它们是最坏的算法。

注意：如果您发现自己无法在少于 n！的时间内按照线性方法解决问题，那么请考虑其他可能产生更好结果的替代方案，例如并行处理、分布式计算或其他更复杂的解决方案。

但除了个人注释之外，一些算法（例如查找值列表的所有排列，甚至计算值的阶乘数）都有非常常见的 O（n！）解决方案。

另外，还有一个非常常见的问题，例如计算斐波那契数列。如果你用递归的方式执行——除非你使用的编程语言支持“尾调用优化”（而 JS 没有），否则在处理非常小的数字时会遇到问题——你会得到一个 O(n!) 算法。

O(nlogn)

我认为理解这个特定的数量级很重要，因为许多常见的算法都属于这个数量级。

尤其是像归并排序、堆排序和快速排序这样的排序算法，其性能表现会如此。这意味着，如果你尝试用它们对足够多的元素进行排序，执行时间将无法优雅地扩展。事实上，它们会持续快速地增加。

许多开发者声称 JavaScript 的Array.sort方法具有 O(nlogn) 的 Big O 复杂度，但实际上，这取决于运行时所使用的实现。例如，Firefox 使用归并排序，因此 O(nlogn) 作为通常的执行复杂度是正确的。然而，例如 V8 运行时（以及 Chrome、Node.js 甚至 Deno）使用 Timsort，它是归并排序和插入排序的混合体，其最佳情况为 O(n)，如果你回到上面的图表，就会发现它要好得多。

在）

图表上的绿线可以理解为：你的算法必须遍历每一个数据点才能完成当前的任务。需要处理的数据点越多，所需的时间就越长。

这些不一定是坏算法，但如果 n 的值（即数据点的数量）会变得相当高，那么你就必须考虑其影响，甚至可能需要某种优化。

经典的 O(n) 算法需要遍历列表的所有元素来执行操作，例如，想象一下必须计算数组中奇数的数量：

function countOdds(list) {

  let totalOdds = 0;
  list.forEach( n => {
    if( n % 2 == 0) totalOdds++;
  });

  return totalOdds;
}

如果数组中有 10 个元素，它会遍历所有元素，而且速度很快。但是，如果数组突然包含 100 万个元素，则需要一段时间，因为其复杂性也会相应增加。

O（logn）

蓝线 (log2n) 表示复杂度虽然会增长，但增长速度缓慢，更妙的是，增长率是有上限的。无论你添加多少数据点，它都不会超过某个值。这是一个非常好的算法，而且它的扩展性相当强。

O(logn) 算法的一个经典示例是二分查找，它不断将问题范围一分为二。

如果您不熟悉该算法，这里有一个快速的介绍，始终假设您正在寻找元素排序列表中的值。

1. 您识别列表中间的元素。
2. 将目标值与中间值进行比较。如果匹配，则完成。否则，继续执行步骤 3。
3. 如果目标低于中间值，则删除右侧列表并从步骤 1 开始对左侧列表重复操作。
4. 如果目标高于中间值，则删除左侧列表并从右侧的步骤 1 开始重复。
5. 重复该过程，直到找到目标或用尽要比较的值。

现在，这个算法的神奇之处在于，如果你增加列表中元素的数量，由于你不断地删除一半，你仍然能够非常快地完成。

例如，在最坏的情况下，如果你有 1,000,000 个元素，你将需要比较 20 次。没错，就是 20 次（这与 的值 13.8 非常接近logn(1000000)）。

如果你仔细想想，你就会发现从 1,000,000 到 20 的过程从 O(n) 变成了 O(logn)。

O(1)

或者像其他人所说的那样是恒定时间。

这是理想的符号，这意味着您将始终能够执行所需的操作，而无需关心必须处理的元素数量。

如果您能够编写一个实现恒定时间的算法，那么它绝对值得投入时间和精力。

举个例子，你可以使用对象字面量，而不是使用多个 IF 语句来决定如何处理你的逻辑。让我用一个例子来解释一下，假设有这样的代码：

function myFunction(myValue) {

  if(myValue == 1) {
    return doOneThing();
  }

  if(myValue == 3) {
    return doAnotherThing();
  }

  if(myValue == 4) {
    return doYetAnotherThing();
  }

  //default behavior
  return doTheDefaultThing(); 
}

最坏的情况是，该代码会检查每个 IF 语句，然后返回默认行为。当然，根据你决定 值的外部逻辑，myValue你可能会认为你的最佳情况要好得多，而且 10 次中有 8 次myValue会得到 1 的值。然而，我们在这里做最坏的打算，却希望得到最好的结果。由于我们有一个算法，它会检查 n 次 的值，所以myValue我们可以说它现在的大 O 符号是 O(n)——请注意，这只适用于非常小的 n 个值，但无论如何，如果你经常调用这个函数，它可能会降低性能。

我们可以改进它吗？我认为可以，我们来看一下：

let logicBehavior = {
  1: doOneThing,
  3: doAnotherThing,
  4: doYetAnotherThing
}

function myFunction(myValue, logic) {
  try {
    logic[myValue]();
  } catch(e) {
    doTheDefaultThing();
  }
}

现在，您可能喜欢也可能不喜欢这个解决方案，但它不再检查每个值。实际上，它直接访问了它应该调用的函数。由于我们做了最坏的打算，在“最坏情况”下，它首先检查索引是否存在于 中logic，然后调用doTheDefaultThing，这将是一个大 O 符号 O(2)，同样，对于可能数百万次的调用来说，这是一个常数，所以我们可以放心地忽略 2，并将其称为 O(1)。

如果你回到一开始的图表，这就是那条粉红线。当然，并非每个算法都能达到 O(1)。

大 O 符号只不过是一个工具而已。它帮助我们比较同一空间内的算法，并一目了然地了解它们的性能，而无需阅读大量相关文档或基准测试。

许多库甚至其他软件产品也会使用这种表示法，Redis 就是一个典型的例子。Redis 的文档中列出了所有命令的大 O 表示法，这有助于你根据它们要处理的记录数量来判断是否应该使用它们。

请记住，这也是一种“最坏情况”类型的测量，在适当的情况下，您仍然可以使用 O(n^2) 算法。

如果您不知道 Big O 是什么意思或者您有任何其他问题，请发表评论，我很乐意帮助您理解这个概念！

如果您喜欢阅读的内容，请考虑加入我的免费时事通讯，以深入了解软件开发职业！ https://fernandodoglio.substack.com